How to find the probability of a 'mean shift' in a random process?
How would I go about calculating the probability that the observed mean of a collection of data generated by a random process, which is governed by a particular statistical model, would deviate from the theoretical mean by a given amount?
For example, the sum of the rolls of two six-sided dice in theory follows a statistical model that resembles a Gaussian probability distribution curve, between the numbers 2 and 12, with a mean of 7. If I was to roll and sum the results of two dice 100 times, how can I calculate the probability that the observed mean of data would be 6, rather than 7?
In other words, if I was to do that test 100 times and the observed mean was calculated to be 6, how can I calculate the probability that the deviation in the mean could be because of random chance, as opposed to the underlying (assumed) statistical model being incorrect (i.e. the dice being biased)?
I know some basic statistics, but I'm far from an expert. I would think that the observed mean of a particular statistical sample would have a probability distribution of its own, but I'm not sure how it could be calculated.
statistics means
add a comment |
How would I go about calculating the probability that the observed mean of a collection of data generated by a random process, which is governed by a particular statistical model, would deviate from the theoretical mean by a given amount?
For example, the sum of the rolls of two six-sided dice in theory follows a statistical model that resembles a Gaussian probability distribution curve, between the numbers 2 and 12, with a mean of 7. If I was to roll and sum the results of two dice 100 times, how can I calculate the probability that the observed mean of data would be 6, rather than 7?
In other words, if I was to do that test 100 times and the observed mean was calculated to be 6, how can I calculate the probability that the deviation in the mean could be because of random chance, as opposed to the underlying (assumed) statistical model being incorrect (i.e. the dice being biased)?
I know some basic statistics, but I'm far from an expert. I would think that the observed mean of a particular statistical sample would have a probability distribution of its own, but I'm not sure how it could be calculated.
statistics means
In the most general case, where the collection elements are from potentially different distributions, and could be dependent, this is very hard to compute. If you know individual variances and covariances, you can compute the variance of the mean, and then give a bound using Chebyshev's inequality.
– Todor Markov
Dec 13 '18 at 8:54
Have also a look at Cramers theorem and large deviation theorems. ocw.mit.edu/courses/sloan-school-of-management/… and ocw.mit.edu/courses/sloan-school-of-management/…
– Thomas
Dec 13 '18 at 11:24
That's the basis of statistics !
– G Cab
Dec 17 '18 at 0:26
add a comment |
How would I go about calculating the probability that the observed mean of a collection of data generated by a random process, which is governed by a particular statistical model, would deviate from the theoretical mean by a given amount?
For example, the sum of the rolls of two six-sided dice in theory follows a statistical model that resembles a Gaussian probability distribution curve, between the numbers 2 and 12, with a mean of 7. If I was to roll and sum the results of two dice 100 times, how can I calculate the probability that the observed mean of data would be 6, rather than 7?
In other words, if I was to do that test 100 times and the observed mean was calculated to be 6, how can I calculate the probability that the deviation in the mean could be because of random chance, as opposed to the underlying (assumed) statistical model being incorrect (i.e. the dice being biased)?
I know some basic statistics, but I'm far from an expert. I would think that the observed mean of a particular statistical sample would have a probability distribution of its own, but I'm not sure how it could be calculated.
statistics means
How would I go about calculating the probability that the observed mean of a collection of data generated by a random process, which is governed by a particular statistical model, would deviate from the theoretical mean by a given amount?
For example, the sum of the rolls of two six-sided dice in theory follows a statistical model that resembles a Gaussian probability distribution curve, between the numbers 2 and 12, with a mean of 7. If I was to roll and sum the results of two dice 100 times, how can I calculate the probability that the observed mean of data would be 6, rather than 7?
In other words, if I was to do that test 100 times and the observed mean was calculated to be 6, how can I calculate the probability that the deviation in the mean could be because of random chance, as opposed to the underlying (assumed) statistical model being incorrect (i.e. the dice being biased)?
I know some basic statistics, but I'm far from an expert. I would think that the observed mean of a particular statistical sample would have a probability distribution of its own, but I'm not sure how it could be calculated.
statistics means
statistics means
asked Dec 10 '18 at 20:39
Time4Tea
27319
27319
In the most general case, where the collection elements are from potentially different distributions, and could be dependent, this is very hard to compute. If you know individual variances and covariances, you can compute the variance of the mean, and then give a bound using Chebyshev's inequality.
– Todor Markov
Dec 13 '18 at 8:54
Have also a look at Cramers theorem and large deviation theorems. ocw.mit.edu/courses/sloan-school-of-management/… and ocw.mit.edu/courses/sloan-school-of-management/…
– Thomas
Dec 13 '18 at 11:24
That's the basis of statistics !
– G Cab
Dec 17 '18 at 0:26
add a comment |
In the most general case, where the collection elements are from potentially different distributions, and could be dependent, this is very hard to compute. If you know individual variances and covariances, you can compute the variance of the mean, and then give a bound using Chebyshev's inequality.
– Todor Markov
Dec 13 '18 at 8:54
Have also a look at Cramers theorem and large deviation theorems. ocw.mit.edu/courses/sloan-school-of-management/… and ocw.mit.edu/courses/sloan-school-of-management/…
– Thomas
Dec 13 '18 at 11:24
That's the basis of statistics !
– G Cab
Dec 17 '18 at 0:26
In the most general case, where the collection elements are from potentially different distributions, and could be dependent, this is very hard to compute. If you know individual variances and covariances, you can compute the variance of the mean, and then give a bound using Chebyshev's inequality.
– Todor Markov
Dec 13 '18 at 8:54
In the most general case, where the collection elements are from potentially different distributions, and could be dependent, this is very hard to compute. If you know individual variances and covariances, you can compute the variance of the mean, and then give a bound using Chebyshev's inequality.
– Todor Markov
Dec 13 '18 at 8:54
Have also a look at Cramers theorem and large deviation theorems. ocw.mit.edu/courses/sloan-school-of-management/… and ocw.mit.edu/courses/sloan-school-of-management/…
– Thomas
Dec 13 '18 at 11:24
Have also a look at Cramers theorem and large deviation theorems. ocw.mit.edu/courses/sloan-school-of-management/… and ocw.mit.edu/courses/sloan-school-of-management/…
– Thomas
Dec 13 '18 at 11:24
That's the basis of statistics !
– G Cab
Dec 17 '18 at 0:26
That's the basis of statistics !
– G Cab
Dec 17 '18 at 0:26
add a comment |
2 Answers
2
active
oldest
votes
Let the random variable $X_i$ denote the outcome of the $i$-th dice roll. Then the observed mean $bar X$ of $n$ dice rolls will simply be their sum $Sigma_X$ divided by the number of rolls $n$, i.e. $$bar X = frac{Sigma_X}n = frac{X_1 + X_2 + dots + X_n}n = frac1n sum_{i=1}^n X_i.$$
This implies that the distribution of $bar X$ is simply the distribution of $Sigma_X$ transformed by uniformly scaling the values of the result by $frac1n$. In particular, the probability that $bar X le 6$, for example, is equal to the probability that $Sigma_X le 6n$.
Now, in your case, each $X_i$ is the sum of the rolls of two six-sided dice, so $Sigma_X$ is simply the sum of $2n$ six-sided dice. This distribution does not (as far as I know) have a common name or any particularly nice algebraic form, although it is closely related to a multinomial distribution with $2n$ trials and six equally likely outcomes per trial. However, it's not particularly hard to calculate it numerically, e.g. by starting with the singular distribution with all probability mass concentrated at zero, and convolving it $2n$ times with the uniform distribution over ${1,2,3,4,5,6}$.
For example, this Python program calculates and prints out the distribution of the sum of 200 six-sided dice, both as the raw point probability of rolling each sum and as the cumulative probability of rolling each sum or less. From the line numbered 600, we can read that the probability of rolling a sum of 600 or less (and thus a mean of 6 or less over 100 pairs of rolls) is approximately 0.00001771.
(Alternatively, we could use a tool made specifically for this job, although we'd need to switch to the export view to get an accurate numerical value for a result so far away from the expected value.)
For large numbers of rolls (say, more than 10) we can also get pretty good results simply by approximating the distribution of $bar X$ (and/or $Sigma_X$) with a normal distribution with the same expectation and variance. This is a consequence of the central limit theorem, which says that the distribution of the sum (and the average) of a large number of identically distributed random variables tends towards a normal distribution.
By the linearity of the expected value, the expected value of $Sigma_X$ is simply the sum of the expected values of the dice rolls, and the expected value of $bar X$ is their average (i.e. the same as for each individual roll, if the rolls are identically distributed). Further, assuming that the dice rolls are independent (or at least uncorrelated), the variance of $Sigma_X$ will be the sum of the variances of the dice rolls, and the variance of $bar X$ will be $frac1{n^2}$ of the variance of $Sigma_X$ (i.e. respectively $n$ and $frac1n$ times the variance of each individual roll, if they're all the same).
Since the variance of a single $k$-sided die roll (i.e. a uniformly distributed random variable over ${1, 2, dots, k}$ is $(k^2-1)mathbin/12$, and the variance of the sum of two rolls is simply twice that, it follows that the variance of a roll of two six-sided dice is $2 times 35 mathbin/ 12 = 35 mathbin/ 6 approx 5.83$. Therefore, over 100 such double rolls, the distribution of the sum $Sigma_X$ is well approximated by a normal distribution with mean $mu = 700$ and variance $sigma^2 approx 583$, while for the average $bar X$, the corresponding parameters are $mu = 7$ and $sigma^2 approx 0.0583$.
One useful feature of this normal approximation is that, for any given deviation of the observed mean from the expected value, we can divide it by the standard deviation $sigma$ of the distribution (which is simply the square root of the variance $sigma^2$) and compare this with a precomputed table of confidence intervals, or a simple diagram like the image below, to see how likely the observed mean is to fall that far from the expectation.
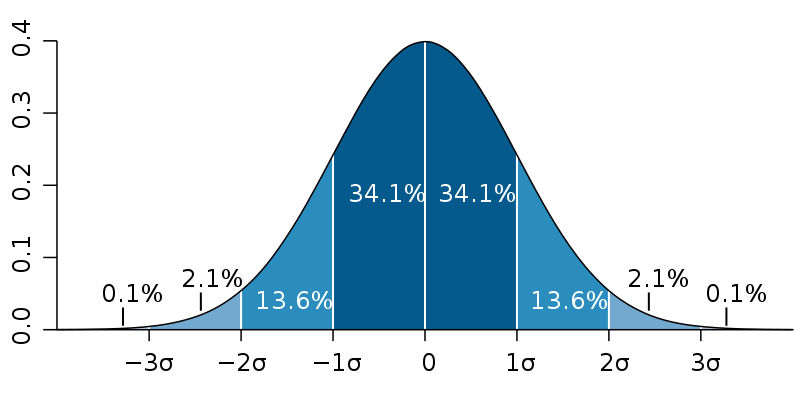
Image from Wikimedia Commons by M. W. Toews, based (in concept) on figure by Jeremy Kemp; used under the CC-By 2.5 license.
For example, the average $bar X$ of 100 rolls of two six-sided dice has a standard deviation of $sigma = sqrt{35 mathbin/ 600} approx 0.2415$. Thus, an observed mean of 6 or less would be $1/sigma approx 4.14 ge 4$ standard deviations below the expected value of 7, and thus (based on the table on the Wikipedia page I linked to above) occurs with probability less than 0.00006334. A more accurate calculation (using the formula $frac12left(1+operatorname{erf}left(frac{x-mu}{sigmasqrt2}right)right)$ also given on the Wikipedia page) yields an approximate probability of 0.0000173 of the observed mean falling this far from the expectation, which is fairly close to the value calculated numerically above without using the normal approximation.
add a comment |
Suppose the game of backgammon is going on, and our task is to understand to what extent the cubes correspond to the ideal statistical model.
Solutions to the problem may be different. Consider them in order of increasing complexity of obtaining the desired result.
$$textbf{Case 1}$$
$textbf{Can be collected separate statistics for each cube.}$
For example, if the cubes differ in appearance.
In this case, the binomial distribution law of
$$P_n(k,p) = binom nm p^m(1-p)^{n-m}$$
should be satisfied, where
$p$ is the probability of the required cube face loss in the single test,
$n$ is the number of throws,
$m$ is the number of depositions of the required face.
For each face of an ideal cube $p=p_r=dfrac16.$
The fact of the loss of a given face $k$ times from $n$ shots denote $E_n(k).$
Let us consider the hypotheses $H_j = left{left|p-dfrac jnright|<dfrac1{2n}right},$
$bigg(p$ belongs to the neighbourhood of value $dfrac jnbigg),$
then
$$P(H_j) = F_n(H_j) = intlimits_{-1/(2n)}^{1/(2n)} P_nleft(m,dfrac jn+xright),mathrm dx,$$
$$P(H_j) = P_nleft(m,dfrac jnright)intlimits_{-1/(2n)}^{1/(2n)}left(dfrac{dfrac jn+x}{dfrac jn}right)^m left(dfrac{dfrac {n-j}n-x}{dfrac{n-j}n}right)^{n-m}dx$$
$$ = dfrac1n P_nleft(m,dfrac jnright)intlimits_{-1/(2n)}^{1/(2n)} left(1+dfrac{nx}jright)^m left(1-dfrac{nx}{n-j}right)^{n-m}d(nx)$$
$$ = dfrac1n P_nleft(m,dfrac jnright)intlimits_{-1/2}^{1/2} left(1+dfrac{y}jright)^m left(1-dfrac{y}{n-j}right)^{n-m}dy.$$
If $quad j>>dfrac12,quad n-j >>dfrac12,quad$ then
$$F_n(H_j) = {smalldfrac1n P_nleft(m,dfrac jnright)intlimits_{-1/2}^{1/2} left(1+dfrac mj y+dfrac{m(m-1)}{2j^2}y^2+dotsright)left(1-dfrac {n-m}{n-j}y+dfrac {(n-m)(n-m-1)}{2(n-j)^2}y^2+dotsright)dy}$$
$$approx dfrac1n P_nleft(m,dfrac jnright)intlimits_{-1/2}^{1/2} left(1+dfrac{(m-j)n}{j(n-j)}y + dfrac{(n^2-n)(j-m)^2+m(n-m)}{2j^2(n-j)^2}y^2right)dy$$
$$ = dfrac jnleft(1+dfrac{(n^2-n)(j-m)^2-mn(n-m)}{24j^2(n-j)^2}right) P_nleft(m,dfrac jnright),$$
The probability of hypothesis for the ideal face of cube is
$$P(H_r) = F_{6k}(k)$$
The plot of the factor
$$1+dfrac{(n^2-n)(j-m)^2-mn(n-m)}{24j^2(n-j)^2}$$
for $m=10,quad n= 60,quad jin(7,15)$

shows that prior probability of hypothesis $H_j$ is
$$P(H_j)approx dfrac 1n P_nleft(m,dfrac jnright)$$
with the accuracy $0.5%.$
Let $n=6m,$ then
begin{cases}
P(E_k | H_r) approx P_{6m}(m,k),\[4pt]
P(E_k | H_j) approx P_{6m}(j,k),\[4pt]
end{cases}
By the Bayesian formula for the posterior probability is
$$P(H_j | E_k) = dfrac{P(E_k | H_j)P(H_j | H_r)}{sum_{j=0}^{6m}P(E_k | H_i)P(H_i |)},$$
$$P(H_j | E_k) = dfrac{dbinom{6m}kleft(dfrac j{6m}right)^kleft(dfrac {6m-j}{6m}right)^{6m-k}{dfrac1{6m}dbinom{6m}j}left(dfrac 16right)^jleft(dfrac 56right)^{6m-j}}
{sumlimits_{i=0}^{6m}dbinom{6m}kleft(dfrac i{6m}right)^kleft(dfrac {6m-i}{6m}right)^{6m-k}dfrac1{6m}dbinom{6m}ileft(dfrac 16right)^ileft(dfrac 56right)^{6m-i}},$$
$$boxed{ P(H_j | E_k) = dfrac{dbinom{6m}j}
{sumlimits_{i=0}^{6m}dbinom{6m}i 5^{j-i} left(dfrac ijright)^kleft(dfrac{6m-i}{6m-j}right)^{6m-k}}},$$
The resulting formula indicates the posterior probability of the distribution of hypotheses about the probability of a given face of a cube falling out, provided that the given face fell $k$ times in $n$ throws
If the given face fell $10$ times in $60$ throws ($m=10, n=60, k=10$), then Wolfram Alpha plot is

If the given face fell $7$ times in $60$ throws ($m=10, n=60, k=7$), then Wolfram Alpha plot is

If the given face fell $15$ times in $60$ throws ($m=10, n=60, k=15$), then Wolfram Alpha plot is

$$textbf{Case 1}$$
$textbf{Can not be collected separate statistics for each cube.}$
This case can not provide valid data, because summation hides individual propertied of cubes. Besides, cubes can be tuned to the combinations as "6+5". Using of this issue data cannot be recommended.
add a comment |
Your Answer
StackExchange.ifUsing("editor", function () {
return StackExchange.using("mathjaxEditing", function () {
StackExchange.MarkdownEditor.creationCallbacks.add(function (editor, postfix) {
StackExchange.mathjaxEditing.prepareWmdForMathJax(editor, postfix, [["$", "$"], ["\\(","\\)"]]);
});
});
}, "mathjax-editing");
StackExchange.ready(function() {
var channelOptions = {
tags: "".split(" "),
id: "69"
};
initTagRenderer("".split(" "), "".split(" "), channelOptions);
StackExchange.using("externalEditor", function() {
// Have to fire editor after snippets, if snippets enabled
if (StackExchange.settings.snippets.snippetsEnabled) {
StackExchange.using("snippets", function() {
createEditor();
});
}
else {
createEditor();
}
});
function createEditor() {
StackExchange.prepareEditor({
heartbeatType: 'answer',
autoActivateHeartbeat: false,
convertImagesToLinks: true,
noModals: true,
showLowRepImageUploadWarning: true,
reputationToPostImages: 10,
bindNavPrevention: true,
postfix: "",
imageUploader: {
brandingHtml: "Powered by u003ca class="icon-imgur-white" href="https://imgur.com/"u003eu003c/au003e",
contentPolicyHtml: "User contributions licensed under u003ca href="https://creativecommons.org/licenses/by-sa/3.0/"u003ecc by-sa 3.0 with attribution requiredu003c/au003e u003ca href="https://stackoverflow.com/legal/content-policy"u003e(content policy)u003c/au003e",
allowUrls: true
},
noCode: true, onDemand: true,
discardSelector: ".discard-answer"
,immediatelyShowMarkdownHelp:true
});
}
});
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function () {
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmath.stackexchange.com%2fquestions%2f3034432%2fhow-to-find-the-probability-of-a-mean-shift-in-a-random-process%23new-answer', 'question_page');
}
);
Post as a guest
Required, but never shown
2 Answers
2
active
oldest
votes
2 Answers
2
active
oldest
votes
active
oldest
votes
active
oldest
votes
Let the random variable $X_i$ denote the outcome of the $i$-th dice roll. Then the observed mean $bar X$ of $n$ dice rolls will simply be their sum $Sigma_X$ divided by the number of rolls $n$, i.e. $$bar X = frac{Sigma_X}n = frac{X_1 + X_2 + dots + X_n}n = frac1n sum_{i=1}^n X_i.$$
This implies that the distribution of $bar X$ is simply the distribution of $Sigma_X$ transformed by uniformly scaling the values of the result by $frac1n$. In particular, the probability that $bar X le 6$, for example, is equal to the probability that $Sigma_X le 6n$.
Now, in your case, each $X_i$ is the sum of the rolls of two six-sided dice, so $Sigma_X$ is simply the sum of $2n$ six-sided dice. This distribution does not (as far as I know) have a common name or any particularly nice algebraic form, although it is closely related to a multinomial distribution with $2n$ trials and six equally likely outcomes per trial. However, it's not particularly hard to calculate it numerically, e.g. by starting with the singular distribution with all probability mass concentrated at zero, and convolving it $2n$ times with the uniform distribution over ${1,2,3,4,5,6}$.
For example, this Python program calculates and prints out the distribution of the sum of 200 six-sided dice, both as the raw point probability of rolling each sum and as the cumulative probability of rolling each sum or less. From the line numbered 600, we can read that the probability of rolling a sum of 600 or less (and thus a mean of 6 or less over 100 pairs of rolls) is approximately 0.00001771.
(Alternatively, we could use a tool made specifically for this job, although we'd need to switch to the export view to get an accurate numerical value for a result so far away from the expected value.)
For large numbers of rolls (say, more than 10) we can also get pretty good results simply by approximating the distribution of $bar X$ (and/or $Sigma_X$) with a normal distribution with the same expectation and variance. This is a consequence of the central limit theorem, which says that the distribution of the sum (and the average) of a large number of identically distributed random variables tends towards a normal distribution.
By the linearity of the expected value, the expected value of $Sigma_X$ is simply the sum of the expected values of the dice rolls, and the expected value of $bar X$ is their average (i.e. the same as for each individual roll, if the rolls are identically distributed). Further, assuming that the dice rolls are independent (or at least uncorrelated), the variance of $Sigma_X$ will be the sum of the variances of the dice rolls, and the variance of $bar X$ will be $frac1{n^2}$ of the variance of $Sigma_X$ (i.e. respectively $n$ and $frac1n$ times the variance of each individual roll, if they're all the same).
Since the variance of a single $k$-sided die roll (i.e. a uniformly distributed random variable over ${1, 2, dots, k}$ is $(k^2-1)mathbin/12$, and the variance of the sum of two rolls is simply twice that, it follows that the variance of a roll of two six-sided dice is $2 times 35 mathbin/ 12 = 35 mathbin/ 6 approx 5.83$. Therefore, over 100 such double rolls, the distribution of the sum $Sigma_X$ is well approximated by a normal distribution with mean $mu = 700$ and variance $sigma^2 approx 583$, while for the average $bar X$, the corresponding parameters are $mu = 7$ and $sigma^2 approx 0.0583$.
One useful feature of this normal approximation is that, for any given deviation of the observed mean from the expected value, we can divide it by the standard deviation $sigma$ of the distribution (which is simply the square root of the variance $sigma^2$) and compare this with a precomputed table of confidence intervals, or a simple diagram like the image below, to see how likely the observed mean is to fall that far from the expectation.

Image from Wikimedia Commons by M. W. Toews, based (in concept) on figure by Jeremy Kemp; used under the CC-By 2.5 license.
For example, the average $bar X$ of 100 rolls of two six-sided dice has a standard deviation of $sigma = sqrt{35 mathbin/ 600} approx 0.2415$. Thus, an observed mean of 6 or less would be $1/sigma approx 4.14 ge 4$ standard deviations below the expected value of 7, and thus (based on the table on the Wikipedia page I linked to above) occurs with probability less than 0.00006334. A more accurate calculation (using the formula $frac12left(1+operatorname{erf}left(frac{x-mu}{sigmasqrt2}right)right)$ also given on the Wikipedia page) yields an approximate probability of 0.0000173 of the observed mean falling this far from the expectation, which is fairly close to the value calculated numerically above without using the normal approximation.
add a comment |
Let the random variable $X_i$ denote the outcome of the $i$-th dice roll. Then the observed mean $bar X$ of $n$ dice rolls will simply be their sum $Sigma_X$ divided by the number of rolls $n$, i.e. $$bar X = frac{Sigma_X}n = frac{X_1 + X_2 + dots + X_n}n = frac1n sum_{i=1}^n X_i.$$
This implies that the distribution of $bar X$ is simply the distribution of $Sigma_X$ transformed by uniformly scaling the values of the result by $frac1n$. In particular, the probability that $bar X le 6$, for example, is equal to the probability that $Sigma_X le 6n$.
Now, in your case, each $X_i$ is the sum of the rolls of two six-sided dice, so $Sigma_X$ is simply the sum of $2n$ six-sided dice. This distribution does not (as far as I know) have a common name or any particularly nice algebraic form, although it is closely related to a multinomial distribution with $2n$ trials and six equally likely outcomes per trial. However, it's not particularly hard to calculate it numerically, e.g. by starting with the singular distribution with all probability mass concentrated at zero, and convolving it $2n$ times with the uniform distribution over ${1,2,3,4,5,6}$.
For example, this Python program calculates and prints out the distribution of the sum of 200 six-sided dice, both as the raw point probability of rolling each sum and as the cumulative probability of rolling each sum or less. From the line numbered 600, we can read that the probability of rolling a sum of 600 or less (and thus a mean of 6 or less over 100 pairs of rolls) is approximately 0.00001771.
(Alternatively, we could use a tool made specifically for this job, although we'd need to switch to the export view to get an accurate numerical value for a result so far away from the expected value.)
For large numbers of rolls (say, more than 10) we can also get pretty good results simply by approximating the distribution of $bar X$ (and/or $Sigma_X$) with a normal distribution with the same expectation and variance. This is a consequence of the central limit theorem, which says that the distribution of the sum (and the average) of a large number of identically distributed random variables tends towards a normal distribution.
By the linearity of the expected value, the expected value of $Sigma_X$ is simply the sum of the expected values of the dice rolls, and the expected value of $bar X$ is their average (i.e. the same as for each individual roll, if the rolls are identically distributed). Further, assuming that the dice rolls are independent (or at least uncorrelated), the variance of $Sigma_X$ will be the sum of the variances of the dice rolls, and the variance of $bar X$ will be $frac1{n^2}$ of the variance of $Sigma_X$ (i.e. respectively $n$ and $frac1n$ times the variance of each individual roll, if they're all the same).
Since the variance of a single $k$-sided die roll (i.e. a uniformly distributed random variable over ${1, 2, dots, k}$ is $(k^2-1)mathbin/12$, and the variance of the sum of two rolls is simply twice that, it follows that the variance of a roll of two six-sided dice is $2 times 35 mathbin/ 12 = 35 mathbin/ 6 approx 5.83$. Therefore, over 100 such double rolls, the distribution of the sum $Sigma_X$ is well approximated by a normal distribution with mean $mu = 700$ and variance $sigma^2 approx 583$, while for the average $bar X$, the corresponding parameters are $mu = 7$ and $sigma^2 approx 0.0583$.
One useful feature of this normal approximation is that, for any given deviation of the observed mean from the expected value, we can divide it by the standard deviation $sigma$ of the distribution (which is simply the square root of the variance $sigma^2$) and compare this with a precomputed table of confidence intervals, or a simple diagram like the image below, to see how likely the observed mean is to fall that far from the expectation.

Image from Wikimedia Commons by M. W. Toews, based (in concept) on figure by Jeremy Kemp; used under the CC-By 2.5 license.
For example, the average $bar X$ of 100 rolls of two six-sided dice has a standard deviation of $sigma = sqrt{35 mathbin/ 600} approx 0.2415$. Thus, an observed mean of 6 or less would be $1/sigma approx 4.14 ge 4$ standard deviations below the expected value of 7, and thus (based on the table on the Wikipedia page I linked to above) occurs with probability less than 0.00006334. A more accurate calculation (using the formula $frac12left(1+operatorname{erf}left(frac{x-mu}{sigmasqrt2}right)right)$ also given on the Wikipedia page) yields an approximate probability of 0.0000173 of the observed mean falling this far from the expectation, which is fairly close to the value calculated numerically above without using the normal approximation.
add a comment |
Let the random variable $X_i$ denote the outcome of the $i$-th dice roll. Then the observed mean $bar X$ of $n$ dice rolls will simply be their sum $Sigma_X$ divided by the number of rolls $n$, i.e. $$bar X = frac{Sigma_X}n = frac{X_1 + X_2 + dots + X_n}n = frac1n sum_{i=1}^n X_i.$$
This implies that the distribution of $bar X$ is simply the distribution of $Sigma_X$ transformed by uniformly scaling the values of the result by $frac1n$. In particular, the probability that $bar X le 6$, for example, is equal to the probability that $Sigma_X le 6n$.
Now, in your case, each $X_i$ is the sum of the rolls of two six-sided dice, so $Sigma_X$ is simply the sum of $2n$ six-sided dice. This distribution does not (as far as I know) have a common name or any particularly nice algebraic form, although it is closely related to a multinomial distribution with $2n$ trials and six equally likely outcomes per trial. However, it's not particularly hard to calculate it numerically, e.g. by starting with the singular distribution with all probability mass concentrated at zero, and convolving it $2n$ times with the uniform distribution over ${1,2,3,4,5,6}$.
For example, this Python program calculates and prints out the distribution of the sum of 200 six-sided dice, both as the raw point probability of rolling each sum and as the cumulative probability of rolling each sum or less. From the line numbered 600, we can read that the probability of rolling a sum of 600 or less (and thus a mean of 6 or less over 100 pairs of rolls) is approximately 0.00001771.
(Alternatively, we could use a tool made specifically for this job, although we'd need to switch to the export view to get an accurate numerical value for a result so far away from the expected value.)
For large numbers of rolls (say, more than 10) we can also get pretty good results simply by approximating the distribution of $bar X$ (and/or $Sigma_X$) with a normal distribution with the same expectation and variance. This is a consequence of the central limit theorem, which says that the distribution of the sum (and the average) of a large number of identically distributed random variables tends towards a normal distribution.
By the linearity of the expected value, the expected value of $Sigma_X$ is simply the sum of the expected values of the dice rolls, and the expected value of $bar X$ is their average (i.e. the same as for each individual roll, if the rolls are identically distributed). Further, assuming that the dice rolls are independent (or at least uncorrelated), the variance of $Sigma_X$ will be the sum of the variances of the dice rolls, and the variance of $bar X$ will be $frac1{n^2}$ of the variance of $Sigma_X$ (i.e. respectively $n$ and $frac1n$ times the variance of each individual roll, if they're all the same).
Since the variance of a single $k$-sided die roll (i.e. a uniformly distributed random variable over ${1, 2, dots, k}$ is $(k^2-1)mathbin/12$, and the variance of the sum of two rolls is simply twice that, it follows that the variance of a roll of two six-sided dice is $2 times 35 mathbin/ 12 = 35 mathbin/ 6 approx 5.83$. Therefore, over 100 such double rolls, the distribution of the sum $Sigma_X$ is well approximated by a normal distribution with mean $mu = 700$ and variance $sigma^2 approx 583$, while for the average $bar X$, the corresponding parameters are $mu = 7$ and $sigma^2 approx 0.0583$.
One useful feature of this normal approximation is that, for any given deviation of the observed mean from the expected value, we can divide it by the standard deviation $sigma$ of the distribution (which is simply the square root of the variance $sigma^2$) and compare this with a precomputed table of confidence intervals, or a simple diagram like the image below, to see how likely the observed mean is to fall that far from the expectation.

Image from Wikimedia Commons by M. W. Toews, based (in concept) on figure by Jeremy Kemp; used under the CC-By 2.5 license.
For example, the average $bar X$ of 100 rolls of two six-sided dice has a standard deviation of $sigma = sqrt{35 mathbin/ 600} approx 0.2415$. Thus, an observed mean of 6 or less would be $1/sigma approx 4.14 ge 4$ standard deviations below the expected value of 7, and thus (based on the table on the Wikipedia page I linked to above) occurs with probability less than 0.00006334. A more accurate calculation (using the formula $frac12left(1+operatorname{erf}left(frac{x-mu}{sigmasqrt2}right)right)$ also given on the Wikipedia page) yields an approximate probability of 0.0000173 of the observed mean falling this far from the expectation, which is fairly close to the value calculated numerically above without using the normal approximation.
Let the random variable $X_i$ denote the outcome of the $i$-th dice roll. Then the observed mean $bar X$ of $n$ dice rolls will simply be their sum $Sigma_X$ divided by the number of rolls $n$, i.e. $$bar X = frac{Sigma_X}n = frac{X_1 + X_2 + dots + X_n}n = frac1n sum_{i=1}^n X_i.$$
This implies that the distribution of $bar X$ is simply the distribution of $Sigma_X$ transformed by uniformly scaling the values of the result by $frac1n$. In particular, the probability that $bar X le 6$, for example, is equal to the probability that $Sigma_X le 6n$.
Now, in your case, each $X_i$ is the sum of the rolls of two six-sided dice, so $Sigma_X$ is simply the sum of $2n$ six-sided dice. This distribution does not (as far as I know) have a common name or any particularly nice algebraic form, although it is closely related to a multinomial distribution with $2n$ trials and six equally likely outcomes per trial. However, it's not particularly hard to calculate it numerically, e.g. by starting with the singular distribution with all probability mass concentrated at zero, and convolving it $2n$ times with the uniform distribution over ${1,2,3,4,5,6}$.
For example, this Python program calculates and prints out the distribution of the sum of 200 six-sided dice, both as the raw point probability of rolling each sum and as the cumulative probability of rolling each sum or less. From the line numbered 600, we can read that the probability of rolling a sum of 600 or less (and thus a mean of 6 or less over 100 pairs of rolls) is approximately 0.00001771.
(Alternatively, we could use a tool made specifically for this job, although we'd need to switch to the export view to get an accurate numerical value for a result so far away from the expected value.)
For large numbers of rolls (say, more than 10) we can also get pretty good results simply by approximating the distribution of $bar X$ (and/or $Sigma_X$) with a normal distribution with the same expectation and variance. This is a consequence of the central limit theorem, which says that the distribution of the sum (and the average) of a large number of identically distributed random variables tends towards a normal distribution.
By the linearity of the expected value, the expected value of $Sigma_X$ is simply the sum of the expected values of the dice rolls, and the expected value of $bar X$ is their average (i.e. the same as for each individual roll, if the rolls are identically distributed). Further, assuming that the dice rolls are independent (or at least uncorrelated), the variance of $Sigma_X$ will be the sum of the variances of the dice rolls, and the variance of $bar X$ will be $frac1{n^2}$ of the variance of $Sigma_X$ (i.e. respectively $n$ and $frac1n$ times the variance of each individual roll, if they're all the same).
Since the variance of a single $k$-sided die roll (i.e. a uniformly distributed random variable over ${1, 2, dots, k}$ is $(k^2-1)mathbin/12$, and the variance of the sum of two rolls is simply twice that, it follows that the variance of a roll of two six-sided dice is $2 times 35 mathbin/ 12 = 35 mathbin/ 6 approx 5.83$. Therefore, over 100 such double rolls, the distribution of the sum $Sigma_X$ is well approximated by a normal distribution with mean $mu = 700$ and variance $sigma^2 approx 583$, while for the average $bar X$, the corresponding parameters are $mu = 7$ and $sigma^2 approx 0.0583$.
One useful feature of this normal approximation is that, for any given deviation of the observed mean from the expected value, we can divide it by the standard deviation $sigma$ of the distribution (which is simply the square root of the variance $sigma^2$) and compare this with a precomputed table of confidence intervals, or a simple diagram like the image below, to see how likely the observed mean is to fall that far from the expectation.

Image from Wikimedia Commons by M. W. Toews, based (in concept) on figure by Jeremy Kemp; used under the CC-By 2.5 license.
For example, the average $bar X$ of 100 rolls of two six-sided dice has a standard deviation of $sigma = sqrt{35 mathbin/ 600} approx 0.2415$. Thus, an observed mean of 6 or less would be $1/sigma approx 4.14 ge 4$ standard deviations below the expected value of 7, and thus (based on the table on the Wikipedia page I linked to above) occurs with probability less than 0.00006334. A more accurate calculation (using the formula $frac12left(1+operatorname{erf}left(frac{x-mu}{sigmasqrt2}right)right)$ also given on the Wikipedia page) yields an approximate probability of 0.0000173 of the observed mean falling this far from the expectation, which is fairly close to the value calculated numerically above without using the normal approximation.
answered Dec 17 '18 at 0:09
Ilmari Karonen
19.4k25182
19.4k25182
add a comment |
add a comment |
Suppose the game of backgammon is going on, and our task is to understand to what extent the cubes correspond to the ideal statistical model.
Solutions to the problem may be different. Consider them in order of increasing complexity of obtaining the desired result.
$$textbf{Case 1}$$
$textbf{Can be collected separate statistics for each cube.}$
For example, if the cubes differ in appearance.
In this case, the binomial distribution law of
$$P_n(k,p) = binom nm p^m(1-p)^{n-m}$$
should be satisfied, where
$p$ is the probability of the required cube face loss in the single test,
$n$ is the number of throws,
$m$ is the number of depositions of the required face.
For each face of an ideal cube $p=p_r=dfrac16.$
The fact of the loss of a given face $k$ times from $n$ shots denote $E_n(k).$
Let us consider the hypotheses $H_j = left{left|p-dfrac jnright|<dfrac1{2n}right},$
$bigg(p$ belongs to the neighbourhood of value $dfrac jnbigg),$
then
$$P(H_j) = F_n(H_j) = intlimits_{-1/(2n)}^{1/(2n)} P_nleft(m,dfrac jn+xright),mathrm dx,$$
$$P(H_j) = P_nleft(m,dfrac jnright)intlimits_{-1/(2n)}^{1/(2n)}left(dfrac{dfrac jn+x}{dfrac jn}right)^m left(dfrac{dfrac {n-j}n-x}{dfrac{n-j}n}right)^{n-m}dx$$
$$ = dfrac1n P_nleft(m,dfrac jnright)intlimits_{-1/(2n)}^{1/(2n)} left(1+dfrac{nx}jright)^m left(1-dfrac{nx}{n-j}right)^{n-m}d(nx)$$
$$ = dfrac1n P_nleft(m,dfrac jnright)intlimits_{-1/2}^{1/2} left(1+dfrac{y}jright)^m left(1-dfrac{y}{n-j}right)^{n-m}dy.$$
If $quad j>>dfrac12,quad n-j >>dfrac12,quad$ then
$$F_n(H_j) = {smalldfrac1n P_nleft(m,dfrac jnright)intlimits_{-1/2}^{1/2} left(1+dfrac mj y+dfrac{m(m-1)}{2j^2}y^2+dotsright)left(1-dfrac {n-m}{n-j}y+dfrac {(n-m)(n-m-1)}{2(n-j)^2}y^2+dotsright)dy}$$
$$approx dfrac1n P_nleft(m,dfrac jnright)intlimits_{-1/2}^{1/2} left(1+dfrac{(m-j)n}{j(n-j)}y + dfrac{(n^2-n)(j-m)^2+m(n-m)}{2j^2(n-j)^2}y^2right)dy$$
$$ = dfrac jnleft(1+dfrac{(n^2-n)(j-m)^2-mn(n-m)}{24j^2(n-j)^2}right) P_nleft(m,dfrac jnright),$$
The probability of hypothesis for the ideal face of cube is
$$P(H_r) = F_{6k}(k)$$
The plot of the factor
$$1+dfrac{(n^2-n)(j-m)^2-mn(n-m)}{24j^2(n-j)^2}$$
for $m=10,quad n= 60,quad jin(7,15)$

shows that prior probability of hypothesis $H_j$ is
$$P(H_j)approx dfrac 1n P_nleft(m,dfrac jnright)$$
with the accuracy $0.5%.$
Let $n=6m,$ then
begin{cases}
P(E_k | H_r) approx P_{6m}(m,k),\[4pt]
P(E_k | H_j) approx P_{6m}(j,k),\[4pt]
end{cases}
By the Bayesian formula for the posterior probability is
$$P(H_j | E_k) = dfrac{P(E_k | H_j)P(H_j | H_r)}{sum_{j=0}^{6m}P(E_k | H_i)P(H_i |)},$$
$$P(H_j | E_k) = dfrac{dbinom{6m}kleft(dfrac j{6m}right)^kleft(dfrac {6m-j}{6m}right)^{6m-k}{dfrac1{6m}dbinom{6m}j}left(dfrac 16right)^jleft(dfrac 56right)^{6m-j}}
{sumlimits_{i=0}^{6m}dbinom{6m}kleft(dfrac i{6m}right)^kleft(dfrac {6m-i}{6m}right)^{6m-k}dfrac1{6m}dbinom{6m}ileft(dfrac 16right)^ileft(dfrac 56right)^{6m-i}},$$
$$boxed{ P(H_j | E_k) = dfrac{dbinom{6m}j}
{sumlimits_{i=0}^{6m}dbinom{6m}i 5^{j-i} left(dfrac ijright)^kleft(dfrac{6m-i}{6m-j}right)^{6m-k}}},$$
The resulting formula indicates the posterior probability of the distribution of hypotheses about the probability of a given face of a cube falling out, provided that the given face fell $k$ times in $n$ throws
If the given face fell $10$ times in $60$ throws ($m=10, n=60, k=10$), then Wolfram Alpha plot is

If the given face fell $7$ times in $60$ throws ($m=10, n=60, k=7$), then Wolfram Alpha plot is

If the given face fell $15$ times in $60$ throws ($m=10, n=60, k=15$), then Wolfram Alpha plot is

$$textbf{Case 1}$$
$textbf{Can not be collected separate statistics for each cube.}$
This case can not provide valid data, because summation hides individual propertied of cubes. Besides, cubes can be tuned to the combinations as "6+5". Using of this issue data cannot be recommended.
add a comment |
Suppose the game of backgammon is going on, and our task is to understand to what extent the cubes correspond to the ideal statistical model.
Solutions to the problem may be different. Consider them in order of increasing complexity of obtaining the desired result.
$$textbf{Case 1}$$
$textbf{Can be collected separate statistics for each cube.}$
For example, if the cubes differ in appearance.
In this case, the binomial distribution law of
$$P_n(k,p) = binom nm p^m(1-p)^{n-m}$$
should be satisfied, where
$p$ is the probability of the required cube face loss in the single test,
$n$ is the number of throws,
$m$ is the number of depositions of the required face.
For each face of an ideal cube $p=p_r=dfrac16.$
The fact of the loss of a given face $k$ times from $n$ shots denote $E_n(k).$
Let us consider the hypotheses $H_j = left{left|p-dfrac jnright|<dfrac1{2n}right},$
$bigg(p$ belongs to the neighbourhood of value $dfrac jnbigg),$
then
$$P(H_j) = F_n(H_j) = intlimits_{-1/(2n)}^{1/(2n)} P_nleft(m,dfrac jn+xright),mathrm dx,$$
$$P(H_j) = P_nleft(m,dfrac jnright)intlimits_{-1/(2n)}^{1/(2n)}left(dfrac{dfrac jn+x}{dfrac jn}right)^m left(dfrac{dfrac {n-j}n-x}{dfrac{n-j}n}right)^{n-m}dx$$
$$ = dfrac1n P_nleft(m,dfrac jnright)intlimits_{-1/(2n)}^{1/(2n)} left(1+dfrac{nx}jright)^m left(1-dfrac{nx}{n-j}right)^{n-m}d(nx)$$
$$ = dfrac1n P_nleft(m,dfrac jnright)intlimits_{-1/2}^{1/2} left(1+dfrac{y}jright)^m left(1-dfrac{y}{n-j}right)^{n-m}dy.$$
If $quad j>>dfrac12,quad n-j >>dfrac12,quad$ then
$$F_n(H_j) = {smalldfrac1n P_nleft(m,dfrac jnright)intlimits_{-1/2}^{1/2} left(1+dfrac mj y+dfrac{m(m-1)}{2j^2}y^2+dotsright)left(1-dfrac {n-m}{n-j}y+dfrac {(n-m)(n-m-1)}{2(n-j)^2}y^2+dotsright)dy}$$
$$approx dfrac1n P_nleft(m,dfrac jnright)intlimits_{-1/2}^{1/2} left(1+dfrac{(m-j)n}{j(n-j)}y + dfrac{(n^2-n)(j-m)^2+m(n-m)}{2j^2(n-j)^2}y^2right)dy$$
$$ = dfrac jnleft(1+dfrac{(n^2-n)(j-m)^2-mn(n-m)}{24j^2(n-j)^2}right) P_nleft(m,dfrac jnright),$$
The probability of hypothesis for the ideal face of cube is
$$P(H_r) = F_{6k}(k)$$
The plot of the factor
$$1+dfrac{(n^2-n)(j-m)^2-mn(n-m)}{24j^2(n-j)^2}$$
for $m=10,quad n= 60,quad jin(7,15)$

shows that prior probability of hypothesis $H_j$ is
$$P(H_j)approx dfrac 1n P_nleft(m,dfrac jnright)$$
with the accuracy $0.5%.$
Let $n=6m,$ then
begin{cases}
P(E_k | H_r) approx P_{6m}(m,k),\[4pt]
P(E_k | H_j) approx P_{6m}(j,k),\[4pt]
end{cases}
By the Bayesian formula for the posterior probability is
$$P(H_j | E_k) = dfrac{P(E_k | H_j)P(H_j | H_r)}{sum_{j=0}^{6m}P(E_k | H_i)P(H_i |)},$$
$$P(H_j | E_k) = dfrac{dbinom{6m}kleft(dfrac j{6m}right)^kleft(dfrac {6m-j}{6m}right)^{6m-k}{dfrac1{6m}dbinom{6m}j}left(dfrac 16right)^jleft(dfrac 56right)^{6m-j}}
{sumlimits_{i=0}^{6m}dbinom{6m}kleft(dfrac i{6m}right)^kleft(dfrac {6m-i}{6m}right)^{6m-k}dfrac1{6m}dbinom{6m}ileft(dfrac 16right)^ileft(dfrac 56right)^{6m-i}},$$
$$boxed{ P(H_j | E_k) = dfrac{dbinom{6m}j}
{sumlimits_{i=0}^{6m}dbinom{6m}i 5^{j-i} left(dfrac ijright)^kleft(dfrac{6m-i}{6m-j}right)^{6m-k}}},$$
The resulting formula indicates the posterior probability of the distribution of hypotheses about the probability of a given face of a cube falling out, provided that the given face fell $k$ times in $n$ throws
If the given face fell $10$ times in $60$ throws ($m=10, n=60, k=10$), then Wolfram Alpha plot is

If the given face fell $7$ times in $60$ throws ($m=10, n=60, k=7$), then Wolfram Alpha plot is

If the given face fell $15$ times in $60$ throws ($m=10, n=60, k=15$), then Wolfram Alpha plot is

$$textbf{Case 1}$$
$textbf{Can not be collected separate statistics for each cube.}$
This case can not provide valid data, because summation hides individual propertied of cubes. Besides, cubes can be tuned to the combinations as "6+5". Using of this issue data cannot be recommended.
add a comment |
Suppose the game of backgammon is going on, and our task is to understand to what extent the cubes correspond to the ideal statistical model.
Solutions to the problem may be different. Consider them in order of increasing complexity of obtaining the desired result.
$$textbf{Case 1}$$
$textbf{Can be collected separate statistics for each cube.}$
For example, if the cubes differ in appearance.
In this case, the binomial distribution law of
$$P_n(k,p) = binom nm p^m(1-p)^{n-m}$$
should be satisfied, where
$p$ is the probability of the required cube face loss in the single test,
$n$ is the number of throws,
$m$ is the number of depositions of the required face.
For each face of an ideal cube $p=p_r=dfrac16.$
The fact of the loss of a given face $k$ times from $n$ shots denote $E_n(k).$
Let us consider the hypotheses $H_j = left{left|p-dfrac jnright|<dfrac1{2n}right},$
$bigg(p$ belongs to the neighbourhood of value $dfrac jnbigg),$
then
$$P(H_j) = F_n(H_j) = intlimits_{-1/(2n)}^{1/(2n)} P_nleft(m,dfrac jn+xright),mathrm dx,$$
$$P(H_j) = P_nleft(m,dfrac jnright)intlimits_{-1/(2n)}^{1/(2n)}left(dfrac{dfrac jn+x}{dfrac jn}right)^m left(dfrac{dfrac {n-j}n-x}{dfrac{n-j}n}right)^{n-m}dx$$
$$ = dfrac1n P_nleft(m,dfrac jnright)intlimits_{-1/(2n)}^{1/(2n)} left(1+dfrac{nx}jright)^m left(1-dfrac{nx}{n-j}right)^{n-m}d(nx)$$
$$ = dfrac1n P_nleft(m,dfrac jnright)intlimits_{-1/2}^{1/2} left(1+dfrac{y}jright)^m left(1-dfrac{y}{n-j}right)^{n-m}dy.$$
If $quad j>>dfrac12,quad n-j >>dfrac12,quad$ then
$$F_n(H_j) = {smalldfrac1n P_nleft(m,dfrac jnright)intlimits_{-1/2}^{1/2} left(1+dfrac mj y+dfrac{m(m-1)}{2j^2}y^2+dotsright)left(1-dfrac {n-m}{n-j}y+dfrac {(n-m)(n-m-1)}{2(n-j)^2}y^2+dotsright)dy}$$
$$approx dfrac1n P_nleft(m,dfrac jnright)intlimits_{-1/2}^{1/2} left(1+dfrac{(m-j)n}{j(n-j)}y + dfrac{(n^2-n)(j-m)^2+m(n-m)}{2j^2(n-j)^2}y^2right)dy$$
$$ = dfrac jnleft(1+dfrac{(n^2-n)(j-m)^2-mn(n-m)}{24j^2(n-j)^2}right) P_nleft(m,dfrac jnright),$$
The probability of hypothesis for the ideal face of cube is
$$P(H_r) = F_{6k}(k)$$
The plot of the factor
$$1+dfrac{(n^2-n)(j-m)^2-mn(n-m)}{24j^2(n-j)^2}$$
for $m=10,quad n= 60,quad jin(7,15)$

shows that prior probability of hypothesis $H_j$ is
$$P(H_j)approx dfrac 1n P_nleft(m,dfrac jnright)$$
with the accuracy $0.5%.$
Let $n=6m,$ then
begin{cases}
P(E_k | H_r) approx P_{6m}(m,k),\[4pt]
P(E_k | H_j) approx P_{6m}(j,k),\[4pt]
end{cases}
By the Bayesian formula for the posterior probability is
$$P(H_j | E_k) = dfrac{P(E_k | H_j)P(H_j | H_r)}{sum_{j=0}^{6m}P(E_k | H_i)P(H_i |)},$$
$$P(H_j | E_k) = dfrac{dbinom{6m}kleft(dfrac j{6m}right)^kleft(dfrac {6m-j}{6m}right)^{6m-k}{dfrac1{6m}dbinom{6m}j}left(dfrac 16right)^jleft(dfrac 56right)^{6m-j}}
{sumlimits_{i=0}^{6m}dbinom{6m}kleft(dfrac i{6m}right)^kleft(dfrac {6m-i}{6m}right)^{6m-k}dfrac1{6m}dbinom{6m}ileft(dfrac 16right)^ileft(dfrac 56right)^{6m-i}},$$
$$boxed{ P(H_j | E_k) = dfrac{dbinom{6m}j}
{sumlimits_{i=0}^{6m}dbinom{6m}i 5^{j-i} left(dfrac ijright)^kleft(dfrac{6m-i}{6m-j}right)^{6m-k}}},$$
The resulting formula indicates the posterior probability of the distribution of hypotheses about the probability of a given face of a cube falling out, provided that the given face fell $k$ times in $n$ throws
If the given face fell $10$ times in $60$ throws ($m=10, n=60, k=10$), then Wolfram Alpha plot is

If the given face fell $7$ times in $60$ throws ($m=10, n=60, k=7$), then Wolfram Alpha plot is

If the given face fell $15$ times in $60$ throws ($m=10, n=60, k=15$), then Wolfram Alpha plot is

$$textbf{Case 1}$$
$textbf{Can not be collected separate statistics for each cube.}$
This case can not provide valid data, because summation hides individual propertied of cubes. Besides, cubes can be tuned to the combinations as "6+5". Using of this issue data cannot be recommended.
Suppose the game of backgammon is going on, and our task is to understand to what extent the cubes correspond to the ideal statistical model.
Solutions to the problem may be different. Consider them in order of increasing complexity of obtaining the desired result.
$$textbf{Case 1}$$
$textbf{Can be collected separate statistics for each cube.}$
For example, if the cubes differ in appearance.
In this case, the binomial distribution law of
$$P_n(k,p) = binom nm p^m(1-p)^{n-m}$$
should be satisfied, where
$p$ is the probability of the required cube face loss in the single test,
$n$ is the number of throws,
$m$ is the number of depositions of the required face.
For each face of an ideal cube $p=p_r=dfrac16.$
The fact of the loss of a given face $k$ times from $n$ shots denote $E_n(k).$
Let us consider the hypotheses $H_j = left{left|p-dfrac jnright|<dfrac1{2n}right},$
$bigg(p$ belongs to the neighbourhood of value $dfrac jnbigg),$
then
$$P(H_j) = F_n(H_j) = intlimits_{-1/(2n)}^{1/(2n)} P_nleft(m,dfrac jn+xright),mathrm dx,$$
$$P(H_j) = P_nleft(m,dfrac jnright)intlimits_{-1/(2n)}^{1/(2n)}left(dfrac{dfrac jn+x}{dfrac jn}right)^m left(dfrac{dfrac {n-j}n-x}{dfrac{n-j}n}right)^{n-m}dx$$
$$ = dfrac1n P_nleft(m,dfrac jnright)intlimits_{-1/(2n)}^{1/(2n)} left(1+dfrac{nx}jright)^m left(1-dfrac{nx}{n-j}right)^{n-m}d(nx)$$
$$ = dfrac1n P_nleft(m,dfrac jnright)intlimits_{-1/2}^{1/2} left(1+dfrac{y}jright)^m left(1-dfrac{y}{n-j}right)^{n-m}dy.$$
If $quad j>>dfrac12,quad n-j >>dfrac12,quad$ then
$$F_n(H_j) = {smalldfrac1n P_nleft(m,dfrac jnright)intlimits_{-1/2}^{1/2} left(1+dfrac mj y+dfrac{m(m-1)}{2j^2}y^2+dotsright)left(1-dfrac {n-m}{n-j}y+dfrac {(n-m)(n-m-1)}{2(n-j)^2}y^2+dotsright)dy}$$
$$approx dfrac1n P_nleft(m,dfrac jnright)intlimits_{-1/2}^{1/2} left(1+dfrac{(m-j)n}{j(n-j)}y + dfrac{(n^2-n)(j-m)^2+m(n-m)}{2j^2(n-j)^2}y^2right)dy$$
$$ = dfrac jnleft(1+dfrac{(n^2-n)(j-m)^2-mn(n-m)}{24j^2(n-j)^2}right) P_nleft(m,dfrac jnright),$$
The probability of hypothesis for the ideal face of cube is
$$P(H_r) = F_{6k}(k)$$
The plot of the factor
$$1+dfrac{(n^2-n)(j-m)^2-mn(n-m)}{24j^2(n-j)^2}$$
for $m=10,quad n= 60,quad jin(7,15)$

shows that prior probability of hypothesis $H_j$ is
$$P(H_j)approx dfrac 1n P_nleft(m,dfrac jnright)$$
with the accuracy $0.5%.$
Let $n=6m,$ then
begin{cases}
P(E_k | H_r) approx P_{6m}(m,k),\[4pt]
P(E_k | H_j) approx P_{6m}(j,k),\[4pt]
end{cases}
By the Bayesian formula for the posterior probability is
$$P(H_j | E_k) = dfrac{P(E_k | H_j)P(H_j | H_r)}{sum_{j=0}^{6m}P(E_k | H_i)P(H_i |)},$$
$$P(H_j | E_k) = dfrac{dbinom{6m}kleft(dfrac j{6m}right)^kleft(dfrac {6m-j}{6m}right)^{6m-k}{dfrac1{6m}dbinom{6m}j}left(dfrac 16right)^jleft(dfrac 56right)^{6m-j}}
{sumlimits_{i=0}^{6m}dbinom{6m}kleft(dfrac i{6m}right)^kleft(dfrac {6m-i}{6m}right)^{6m-k}dfrac1{6m}dbinom{6m}ileft(dfrac 16right)^ileft(dfrac 56right)^{6m-i}},$$
$$boxed{ P(H_j | E_k) = dfrac{dbinom{6m}j}
{sumlimits_{i=0}^{6m}dbinom{6m}i 5^{j-i} left(dfrac ijright)^kleft(dfrac{6m-i}{6m-j}right)^{6m-k}}},$$
The resulting formula indicates the posterior probability of the distribution of hypotheses about the probability of a given face of a cube falling out, provided that the given face fell $k$ times in $n$ throws
If the given face fell $10$ times in $60$ throws ($m=10, n=60, k=10$), then Wolfram Alpha plot is

If the given face fell $7$ times in $60$ throws ($m=10, n=60, k=7$), then Wolfram Alpha plot is

If the given face fell $15$ times in $60$ throws ($m=10, n=60, k=15$), then Wolfram Alpha plot is

$$textbf{Case 1}$$
$textbf{Can not be collected separate statistics for each cube.}$
This case can not provide valid data, because summation hides individual propertied of cubes. Besides, cubes can be tuned to the combinations as "6+5". Using of this issue data cannot be recommended.
answered Dec 18 '18 at 22:14
Yuri Negometyanov
10.8k1726
10.8k1726
add a comment |
add a comment |
Thanks for contributing an answer to Mathematics Stack Exchange!
- Please be sure to answer the question. Provide details and share your research!
But avoid …
- Asking for help, clarification, or responding to other answers.
- Making statements based on opinion; back them up with references or personal experience.
Use MathJax to format equations. MathJax reference.
To learn more, see our tips on writing great answers.
Some of your past answers have not been well-received, and you're in danger of being blocked from answering.
Please pay close attention to the following guidance:
- Please be sure to answer the question. Provide details and share your research!
But avoid …
- Asking for help, clarification, or responding to other answers.
- Making statements based on opinion; back them up with references or personal experience.
To learn more, see our tips on writing great answers.
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function () {
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmath.stackexchange.com%2fquestions%2f3034432%2fhow-to-find-the-probability-of-a-mean-shift-in-a-random-process%23new-answer', 'question_page');
}
);
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
In the most general case, where the collection elements are from potentially different distributions, and could be dependent, this is very hard to compute. If you know individual variances and covariances, you can compute the variance of the mean, and then give a bound using Chebyshev's inequality.
– Todor Markov
Dec 13 '18 at 8:54
Have also a look at Cramers theorem and large deviation theorems. ocw.mit.edu/courses/sloan-school-of-management/… and ocw.mit.edu/courses/sloan-school-of-management/…
– Thomas
Dec 13 '18 at 11:24
That's the basis of statistics !
– G Cab
Dec 17 '18 at 0:26