Is there a koch circle?
$begingroup$
Is there some fractal like the koch snowflake, but only with many circles around a bigger initial circle, each of them surrounded by smaller circles and so on (but all of them kissing one bigger circle)? So circles instead of the triangles in a koch snowflake... If not, why?
fractals
asked Feb 9 '15 at 19:04
user2103480user2103480
689617
$endgroup$
add a comment |
$begingroup$
Is there some fractal like the koch snowflake, but only with many circles around a bigger initial circle, each of them surrounded by smaller circles and so on (but all of them kissing one bigger circle)? So circles instead of the triangles in a koch snowflake... If not, why?
fractals
asked Feb 9 '15 at 19:04
user2103480user2103480
689617
$endgroup$
4
$begingroup$
I'm not sure of all the details you want, but anything you can imagine or roughly draw could certainly be "fractalized", but there remains the question of why someone would want to study it. Possible close to what you want might be Apollonian Gasket, however.
$endgroup$
– Dave L. Renfro
Feb 9 '15 at 19:35
1
$begingroup$
An apollonian gasket comes close to what I imagine, yes! I honestly don't know a reason to study it, aside that it maybe beautiful(probably not as beautiful as the gasket).
$endgroup$
– user2103480
Feb 9 '15 at 20:27
$begingroup$
Apollonian Gasket seems like the best answer so far.
$endgroup$
– alan2here
May 21 '17 at 17:42
add a comment |
$begingroup$
Is there some fractal like the koch snowflake, but only with many circles around a bigger initial circle, each of them surrounded by smaller circles and so on (but all of them kissing one bigger circle)? So circles instead of the triangles in a koch snowflake... If not, why?
fractals
asked Feb 9 '15 at 19:04
user2103480user2103480
689617
$endgroup$
Is there some fractal like the koch snowflake, but only with many circles around a bigger initial circle, each of them surrounded by smaller circles and so on (but all of them kissing one bigger circle)? So circles instead of the triangles in a koch snowflake... If not, why?
fractals
fractals
asked Feb 9 '15 at 19:04
user2103480user2103480
689617
asked Feb 9 '15 at 19:04
user2103480user2103480
689617
asked Feb 9 '15 at 19:04
user2103480user2103480
689617
asked Feb 9 '15 at 19:04
user2103480user2103480
689617
asked Feb 9 '15 at 19:04
user2103480user2103480
689617
689617
4
$begingroup$
I'm not sure of all the details you want, but anything you can imagine or roughly draw could certainly be "fractalized", but there remains the question of why someone would want to study it. Possible close to what you want might be Apollonian Gasket, however.
$endgroup$
– Dave L. Renfro
Feb 9 '15 at 19:35
1
$begingroup$
An apollonian gasket comes close to what I imagine, yes! I honestly don't know a reason to study it, aside that it maybe beautiful(probably not as beautiful as the gasket).
$endgroup$
– user2103480
Feb 9 '15 at 20:27
$begingroup$
Apollonian Gasket seems like the best answer so far.
$endgroup$
– alan2here
May 21 '17 at 17:42
add a comment |
4
$begingroup$
I'm not sure of all the details you want, but anything you can imagine or roughly draw could certainly be "fractalized", but there remains the question of why someone would want to study it. Possible close to what you want might be Apollonian Gasket, however.
$endgroup$
– Dave L. Renfro
Feb 9 '15 at 19:35
1
$begingroup$
An apollonian gasket comes close to what I imagine, yes! I honestly don't know a reason to study it, aside that it maybe beautiful(probably not as beautiful as the gasket).
$endgroup$
– user2103480
Feb 9 '15 at 20:27
$begingroup$
Apollonian Gasket seems like the best answer so far.
$endgroup$
– alan2here
May 21 '17 at 17:42
4
4
$begingroup$
I'm not sure of all the details you want, but anything you can imagine or roughly draw could certainly be "fractalized", but there remains the question of why someone would want to study it. Possible close to what you want might be Apollonian Gasket, however.
$endgroup$
– Dave L. Renfro
Feb 9 '15 at 19:35
$begingroup$
I'm not sure of all the details you want, but anything you can imagine or roughly draw could certainly be "fractalized", but there remains the question of why someone would want to study it. Possible close to what you want might be Apollonian Gasket, however.
$endgroup$
– Dave L. Renfro
Feb 9 '15 at 19:35
1
1
$begingroup$
An apollonian gasket comes close to what I imagine, yes! I honestly don't know a reason to study it, aside that it maybe beautiful(probably not as beautiful as the gasket).
$endgroup$
– user2103480
Feb 9 '15 at 20:27
$begingroup$
An apollonian gasket comes close to what I imagine, yes! I honestly don't know a reason to study it, aside that it maybe beautiful(probably not as beautiful as the gasket).
$endgroup$
– user2103480
Feb 9 '15 at 20:27
$begingroup$
Apollonian Gasket seems like the best answer so far.
$endgroup$
– alan2here
May 21 '17 at 17:42
$begingroup$
Apollonian Gasket seems like the best answer so far.
$endgroup$
– alan2here
May 21 '17 at 17:42
add a comment |
4 Answers
4
active
oldest
votes
$begingroup$
Is this any good?
It's the last frame in the animation for this answer.
edited Apr 13 '17 at 12:21
Community♦
1
answered Feb 10 '15 at 6:12
Mark McClureMark McClure
23.9k34472
$endgroup$
2
$begingroup$
I think this is definitely the closest out of the three answers to matching the spirit of OP's question. It's very mesmerizing. +1
$endgroup$
– Cameron Williams
Feb 10 '15 at 6:15
$begingroup$
Yes, I'll chose this as the answer! Almost exactly as I imagined it... but more beautiful! I liked the other answers too, though :)
$endgroup$
– user2103480
Feb 10 '15 at 14:10
add a comment |
$begingroup$
Parts of the Mandelbrot set look like circles with smaller circles attached recursively:
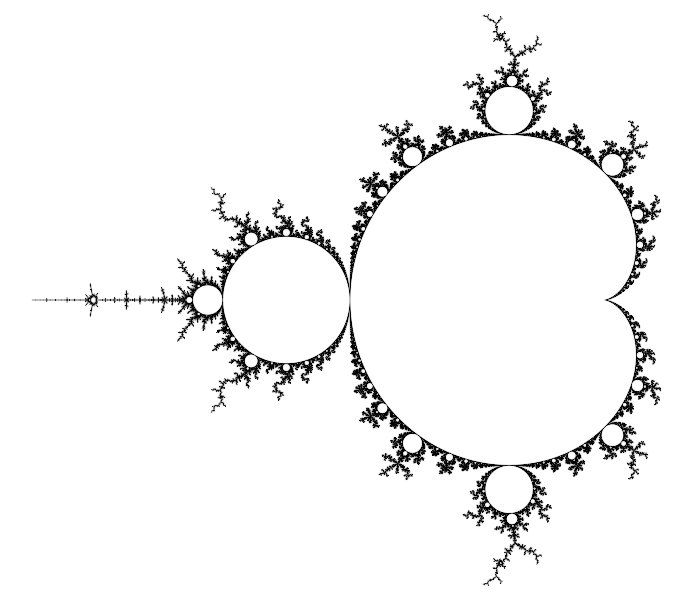
They aren't quite exact circles (except for the one centered at $-1+0i$), but the property that the radius of the smaller circle attached at rational angle $frac{p}{q}$ measured in turns is approximately $q^2$ times smaller provides a way to construct a similar fractal from exact circles:
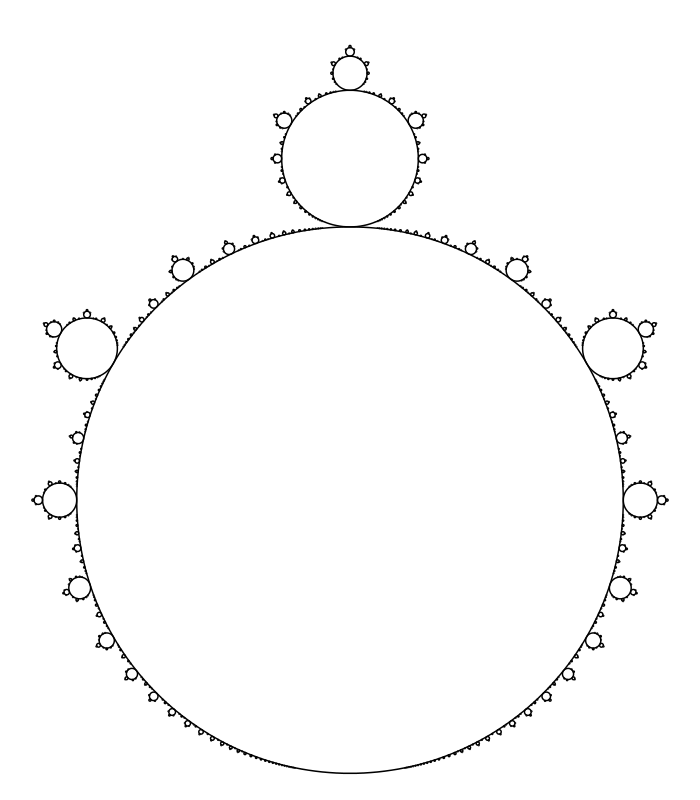
Haskell source code using the Diagrams library:
import Diagrams.Prelude
import Diagrams.Backend.SVG.CmdLine (defaultMain)
main
= defaultMain
$ diagram 1
# rotateBy (-0.25)
# pad 1.1
# lw thin
# bg white
power = 2
minimumRadius = 0.001
diagram radius
| radius < minimumRadius = mempty
| otherwise = circle radius <> mconcat
[ diagram r
# rotateBy (s - 0.5)
# translate (r2 (rr * cos t, rr * sin t))
| den <- [ 2 .. ceiling (sqrt (radius / minimumRadius)) ]
, num <- [ 1 .. den - 1 ]
, num `gcd` den == 1
, let s = fi num / fi den
, let t = 2 * pi * s
, let r = radius / fi den ** power
, let rr = radius + r
]
where
fi = fromInteger
Reducing the power makes the circles larger, but too low and they eventually overlap - in any case the power must be larger than one to ensure the circles actually do get smaller.
edited Mar 9 '17 at 17:32
Community♦
1
answered Feb 9 '15 at 20:35
ClaudeClaude
2,595523
$endgroup$
$begingroup$
(+1) Thanks for the code :) Circles overlaping was a concern of mine, too - you found a real nice reduction to what I was looking for!
$endgroup$
– user2103480
Feb 9 '15 at 20:46
$begingroup$
Can you link a version of the 2nd picture here where the power is set such that the circles get smaller as gradually as they can without overlapping?
$endgroup$
– alan2here
May 14 '17 at 19:52
1
$begingroup$
@alan2here I suspect that the minimal power without overlap is in fact $2$, as in the picture, though I haven't a proof yet. Maybe the fact that $operatorname{exsec} theta approx frac{1}{2}theta^2$ has something to do with it?
$endgroup$
– Claude
May 16 '17 at 16:25
$begingroup$
commons.wikimedia.org/wiki/…
$endgroup$
– Adam
Jan 1 at 19:39
add a comment |
$begingroup$
Maybe the "Pharaoh's Breastplate" described by Mandelbrot.
Here plotted by Ken Monks
answered Feb 9 '15 at 21:11
GEdgarGEdgar
63.7k269176
$endgroup$
add a comment |
$begingroup$
If you draw 6 smaller circles inside each circle you draw... you end up with something like a
My rendering only draws 6 iterations deep - but you could theoretically go forever.
edited Jan 14 at 22:02
Xander Henderson
15.2k103556
answered Jan 14 at 21:31
Tom HTom H
111
$endgroup$
1
$begingroup$
That construction is usually called the "hexagasket". It is a specific example of a general construction called an "$n$-gasket" (in case you are looking for things to Google).
$endgroup$
– Xander Henderson
Jan 14 at 22:01
add a comment |
Your Answer
StackExchange.ready(function() {
var channelOptions = {
tags: "".split(" "),
id: "69"
};
initTagRenderer("".split(" "), "".split(" "), channelOptions);
StackExchange.using("externalEditor", function() {
// Have to fire editor after snippets, if snippets enabled
if (StackExchange.settings.snippets.snippetsEnabled) {
StackExchange.using("snippets", function() {
createEditor();
});
}
else {
createEditor();
}
});
function createEditor() {
StackExchange.prepareEditor({
heartbeatType: 'answer',
autoActivateHeartbeat: false,
convertImagesToLinks: true,
noModals: true,
showLowRepImageUploadWarning: true,
reputationToPostImages: 10,
bindNavPrevention: true,
postfix: "",
imageUploader: {
brandingHtml: "Powered by u003ca class="icon-imgur-white" href="https://imgur.com/"u003eu003c/au003e",
contentPolicyHtml: "User contributions licensed under u003ca href="https://creativecommons.org/licenses/by-sa/3.0/"u003ecc by-sa 3.0 with attribution requiredu003c/au003e u003ca href="https://stackoverflow.com/legal/content-policy"u003e(content policy)u003c/au003e",
allowUrls: true
},
noCode: true, onDemand: true,
discardSelector: ".discard-answer"
,immediatelyShowMarkdownHelp:true
});
}
});
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function () {
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmath.stackexchange.com%2fquestions%2f1140989%2fis-there-a-koch-circle%23new-answer', 'question_page');
}
);
Post as a guest
Required, but never shown
4 Answers
4
active
oldest
votes
4 Answers
4
active
oldest
votes
active
oldest
votes
active
oldest
votes
$begingroup$
Is this any good?
It's the last frame in the animation for this answer.
edited Apr 13 '17 at 12:21
Community♦
1
answered Feb 10 '15 at 6:12
Mark McClureMark McClure
23.9k34472
$endgroup$
2
$begingroup$
I think this is definitely the closest out of the three answers to matching the spirit of OP's question. It's very mesmerizing. +1
$endgroup$
– Cameron Williams
Feb 10 '15 at 6:15
$begingroup$
Yes, I'll chose this as the answer! Almost exactly as I imagined it... but more beautiful! I liked the other answers too, though :)
$endgroup$
– user2103480
Feb 10 '15 at 14:10
add a comment |
$begingroup$
Is this any good?
It's the last frame in the animation for this answer.
edited Apr 13 '17 at 12:21
Community♦
1
answered Feb 10 '15 at 6:12
Mark McClureMark McClure
23.9k34472
$endgroup$
2
$begingroup$
I think this is definitely the closest out of the three answers to matching the spirit of OP's question. It's very mesmerizing. +1
$endgroup$
– Cameron Williams
Feb 10 '15 at 6:15
$begingroup$
Yes, I'll chose this as the answer! Almost exactly as I imagined it... but more beautiful! I liked the other answers too, though :)
$endgroup$
– user2103480
Feb 10 '15 at 14:10
add a comment |
$begingroup$
Is this any good?
It's the last frame in the animation for this answer.
edited Apr 13 '17 at 12:21
Community♦
1
answered Feb 10 '15 at 6:12
Mark McClureMark McClure
23.9k34472
$endgroup$
Is this any good?
It's the last frame in the animation for this answer.
edited Apr 13 '17 at 12:21
Community♦
1
answered Feb 10 '15 at 6:12
Mark McClureMark McClure
23.9k34472
edited Apr 13 '17 at 12:21
Community♦
1
edited Apr 13 '17 at 12:21
Community♦
1
edited Apr 13 '17 at 12:21
Community♦
1
1
answered Feb 10 '15 at 6:12
Mark McClureMark McClure
23.9k34472
answered Feb 10 '15 at 6:12
Mark McClureMark McClure
23.9k34472
answered Feb 10 '15 at 6:12
Mark McClureMark McClure
23.9k34472
23.9k34472
2
$begingroup$
I think this is definitely the closest out of the three answers to matching the spirit of OP's question. It's very mesmerizing. +1
$endgroup$
– Cameron Williams
Feb 10 '15 at 6:15
$begingroup$
Yes, I'll chose this as the answer! Almost exactly as I imagined it... but more beautiful! I liked the other answers too, though :)
$endgroup$
– user2103480
Feb 10 '15 at 14:10
add a comment |
2
$begingroup$
I think this is definitely the closest out of the three answers to matching the spirit of OP's question. It's very mesmerizing. +1
$endgroup$
– Cameron Williams
Feb 10 '15 at 6:15
$begingroup$
Yes, I'll chose this as the answer! Almost exactly as I imagined it... but more beautiful! I liked the other answers too, though :)
$endgroup$
– user2103480
Feb 10 '15 at 14:10
2
2
$begingroup$
I think this is definitely the closest out of the three answers to matching the spirit of OP's question. It's very mesmerizing. +1
$endgroup$
– Cameron Williams
Feb 10 '15 at 6:15
$begingroup$
I think this is definitely the closest out of the three answers to matching the spirit of OP's question. It's very mesmerizing. +1
$endgroup$
– Cameron Williams
Feb 10 '15 at 6:15
$begingroup$
Yes, I'll chose this as the answer! Almost exactly as I imagined it... but more beautiful! I liked the other answers too, though :)
$endgroup$
– user2103480
Feb 10 '15 at 14:10
$begingroup$
Yes, I'll chose this as the answer! Almost exactly as I imagined it... but more beautiful! I liked the other answers too, though :)
$endgroup$
– user2103480
Feb 10 '15 at 14:10
add a comment |
$begingroup$
Parts of the Mandelbrot set look like circles with smaller circles attached recursively:
They aren't quite exact circles (except for the one centered at $-1+0i$), but the property that the radius of the smaller circle attached at rational angle $frac{p}{q}$ measured in turns is approximately $q^2$ times smaller provides a way to construct a similar fractal from exact circles:
Haskell source code using the Diagrams library:
import Diagrams.Prelude
import Diagrams.Backend.SVG.CmdLine (defaultMain)
main
= defaultMain
$ diagram 1
# rotateBy (-0.25)
# pad 1.1
# lw thin
# bg white
power = 2
minimumRadius = 0.001
diagram radius
| radius < minimumRadius = mempty
| otherwise = circle radius <> mconcat
[ diagram r
# rotateBy (s - 0.5)
# translate (r2 (rr * cos t, rr * sin t))
| den <- [ 2 .. ceiling (sqrt (radius / minimumRadius)) ]
, num <- [ 1 .. den - 1 ]
, num `gcd` den == 1
, let s = fi num / fi den
, let t = 2 * pi * s
, let r = radius / fi den ** power
, let rr = radius + r
]
where
fi = fromInteger
Reducing the power makes the circles larger, but too low and they eventually overlap - in any case the power must be larger than one to ensure the circles actually do get smaller.
edited Mar 9 '17 at 17:32
Community♦
1
answered Feb 9 '15 at 20:35
ClaudeClaude
2,595523
$endgroup$
$begingroup$
(+1) Thanks for the code :) Circles overlaping was a concern of mine, too - you found a real nice reduction to what I was looking for!
$endgroup$
– user2103480
Feb 9 '15 at 20:46
$begingroup$
Can you link a version of the 2nd picture here where the power is set such that the circles get smaller as gradually as they can without overlapping?
$endgroup$
– alan2here
May 14 '17 at 19:52
1
$begingroup$
@alan2here I suspect that the minimal power without overlap is in fact $2$, as in the picture, though I haven't a proof yet. Maybe the fact that $operatorname{exsec} theta approx frac{1}{2}theta^2$ has something to do with it?
$endgroup$
– Claude
May 16 '17 at 16:25
$begingroup$
commons.wikimedia.org/wiki/…
$endgroup$
– Adam
Jan 1 at 19:39
add a comment |
$begingroup$
Parts of the Mandelbrot set look like circles with smaller circles attached recursively:
They aren't quite exact circles (except for the one centered at $-1+0i$), but the property that the radius of the smaller circle attached at rational angle $frac{p}{q}$ measured in turns is approximately $q^2$ times smaller provides a way to construct a similar fractal from exact circles:
Haskell source code using the Diagrams library:
import Diagrams.Prelude
import Diagrams.Backend.SVG.CmdLine (defaultMain)
main
= defaultMain
$ diagram 1
# rotateBy (-0.25)
# pad 1.1
# lw thin
# bg white
power = 2
minimumRadius = 0.001
diagram radius
| radius < minimumRadius = mempty
| otherwise = circle radius <> mconcat
[ diagram r
# rotateBy (s - 0.5)
# translate (r2 (rr * cos t, rr * sin t))
| den <- [ 2 .. ceiling (sqrt (radius / minimumRadius)) ]
, num <- [ 1 .. den - 1 ]
, num `gcd` den == 1
, let s = fi num / fi den
, let t = 2 * pi * s
, let r = radius / fi den ** power
, let rr = radius + r
]
where
fi = fromInteger
Reducing the power makes the circles larger, but too low and they eventually overlap - in any case the power must be larger than one to ensure the circles actually do get smaller.
edited Mar 9 '17 at 17:32
Community♦
1
answered Feb 9 '15 at 20:35
ClaudeClaude
2,595523
$endgroup$
$begingroup$
(+1) Thanks for the code :) Circles overlaping was a concern of mine, too - you found a real nice reduction to what I was looking for!
$endgroup$
– user2103480
Feb 9 '15 at 20:46
$begingroup$
Can you link a version of the 2nd picture here where the power is set such that the circles get smaller as gradually as they can without overlapping?
$endgroup$
– alan2here
May 14 '17 at 19:52
1
$begingroup$
@alan2here I suspect that the minimal power without overlap is in fact $2$, as in the picture, though I haven't a proof yet. Maybe the fact that $operatorname{exsec} theta approx frac{1}{2}theta^2$ has something to do with it?
$endgroup$
– Claude
May 16 '17 at 16:25
$begingroup$
commons.wikimedia.org/wiki/…
$endgroup$
– Adam
Jan 1 at 19:39
add a comment |
$begingroup$
Parts of the Mandelbrot set look like circles with smaller circles attached recursively:
They aren't quite exact circles (except for the one centered at $-1+0i$), but the property that the radius of the smaller circle attached at rational angle $frac{p}{q}$ measured in turns is approximately $q^2$ times smaller provides a way to construct a similar fractal from exact circles:
Haskell source code using the Diagrams library:
import Diagrams.Prelude
import Diagrams.Backend.SVG.CmdLine (defaultMain)
main
= defaultMain
$ diagram 1
# rotateBy (-0.25)
# pad 1.1
# lw thin
# bg white
power = 2
minimumRadius = 0.001
diagram radius
| radius < minimumRadius = mempty
| otherwise = circle radius <> mconcat
[ diagram r
# rotateBy (s - 0.5)
# translate (r2 (rr * cos t, rr * sin t))
| den <- [ 2 .. ceiling (sqrt (radius / minimumRadius)) ]
, num <- [ 1 .. den - 1 ]
, num `gcd` den == 1
, let s = fi num / fi den
, let t = 2 * pi * s
, let r = radius / fi den ** power
, let rr = radius + r
]
where
fi = fromInteger
Reducing the power makes the circles larger, but too low and they eventually overlap - in any case the power must be larger than one to ensure the circles actually do get smaller.
edited Mar 9 '17 at 17:32
Community♦
1
answered Feb 9 '15 at 20:35
ClaudeClaude
2,595523
$endgroup$
Parts of the Mandelbrot set look like circles with smaller circles attached recursively:
They aren't quite exact circles (except for the one centered at $-1+0i$), but the property that the radius of the smaller circle attached at rational angle $frac{p}{q}$ measured in turns is approximately $q^2$ times smaller provides a way to construct a similar fractal from exact circles:
Haskell source code using the Diagrams library:
import Diagrams.Prelude
import Diagrams.Backend.SVG.CmdLine (defaultMain)
main
= defaultMain
$ diagram 1
# rotateBy (-0.25)
# pad 1.1
# lw thin
# bg white
power = 2
minimumRadius = 0.001
diagram radius
| radius < minimumRadius = mempty
| otherwise = circle radius <> mconcat
[ diagram r
# rotateBy (s - 0.5)
# translate (r2 (rr * cos t, rr * sin t))
| den <- [ 2 .. ceiling (sqrt (radius / minimumRadius)) ]
, num <- [ 1 .. den - 1 ]
, num `gcd` den == 1
, let s = fi num / fi den
, let t = 2 * pi * s
, let r = radius / fi den ** power
, let rr = radius + r
]
where
fi = fromInteger
Reducing the power makes the circles larger, but too low and they eventually overlap - in any case the power must be larger than one to ensure the circles actually do get smaller.
edited Mar 9 '17 at 17:32
Community♦
1
answered Feb 9 '15 at 20:35
ClaudeClaude
2,595523
edited Mar 9 '17 at 17:32
Community♦
1
edited Mar 9 '17 at 17:32
Community♦
1
edited Mar 9 '17 at 17:32
Community♦
1
1
answered Feb 9 '15 at 20:35
ClaudeClaude
2,595523
answered Feb 9 '15 at 20:35
ClaudeClaude
2,595523
answered Feb 9 '15 at 20:35
ClaudeClaude
2,595523
2,595523
$begingroup$
(+1) Thanks for the code :) Circles overlaping was a concern of mine, too - you found a real nice reduction to what I was looking for!
$endgroup$
– user2103480
Feb 9 '15 at 20:46
$begingroup$
Can you link a version of the 2nd picture here where the power is set such that the circles get smaller as gradually as they can without overlapping?
$endgroup$
– alan2here
May 14 '17 at 19:52
1
$begingroup$
@alan2here I suspect that the minimal power without overlap is in fact $2$, as in the picture, though I haven't a proof yet. Maybe the fact that $operatorname{exsec} theta approx frac{1}{2}theta^2$ has something to do with it?
$endgroup$
– Claude
May 16 '17 at 16:25
$begingroup$
commons.wikimedia.org/wiki/…
$endgroup$
– Adam
Jan 1 at 19:39
add a comment |
$begingroup$
(+1) Thanks for the code :) Circles overlaping was a concern of mine, too - you found a real nice reduction to what I was looking for!
$endgroup$
– user2103480
Feb 9 '15 at 20:46
$begingroup$
Can you link a version of the 2nd picture here where the power is set such that the circles get smaller as gradually as they can without overlapping?
$endgroup$
– alan2here
May 14 '17 at 19:52
1
$begingroup$
@alan2here I suspect that the minimal power without overlap is in fact $2$, as in the picture, though I haven't a proof yet. Maybe the fact that $operatorname{exsec} theta approx frac{1}{2}theta^2$ has something to do with it?
$endgroup$
– Claude
May 16 '17 at 16:25
$begingroup$
commons.wikimedia.org/wiki/…
$endgroup$
– Adam
Jan 1 at 19:39
$begingroup$
(+1) Thanks for the code :) Circles overlaping was a concern of mine, too - you found a real nice reduction to what I was looking for!
$endgroup$
– user2103480
Feb 9 '15 at 20:46
$begingroup$
(+1) Thanks for the code :) Circles overlaping was a concern of mine, too - you found a real nice reduction to what I was looking for!
$endgroup$
– user2103480
Feb 9 '15 at 20:46
$begingroup$
Can you link a version of the 2nd picture here where the power is set such that the circles get smaller as gradually as they can without overlapping?
$endgroup$
– alan2here
May 14 '17 at 19:52
$begingroup$
Can you link a version of the 2nd picture here where the power is set such that the circles get smaller as gradually as they can without overlapping?
$endgroup$
– alan2here
May 14 '17 at 19:52
1
1
$begingroup$
@alan2here I suspect that the minimal power without overlap is in fact $2$, as in the picture, though I haven't a proof yet. Maybe the fact that $operatorname{exsec} theta approx frac{1}{2}theta^2$ has something to do with it?
$endgroup$
– Claude
May 16 '17 at 16:25
$begingroup$
@alan2here I suspect that the minimal power without overlap is in fact $2$, as in the picture, though I haven't a proof yet. Maybe the fact that $operatorname{exsec} theta approx frac{1}{2}theta^2$ has something to do with it?
$endgroup$
– Claude
May 16 '17 at 16:25
$begingroup$
commons.wikimedia.org/wiki/…
$endgroup$
– Adam
Jan 1 at 19:39
$begingroup$
commons.wikimedia.org/wiki/…
$endgroup$
– Adam
Jan 1 at 19:39
add a comment |
$begingroup$
Maybe the "Pharaoh's Breastplate" described by Mandelbrot.
Here plotted by Ken Monks
answered Feb 9 '15 at 21:11
GEdgarGEdgar
63.7k269176
$endgroup$
add a comment |
$begingroup$
Maybe the "Pharaoh's Breastplate" described by Mandelbrot.
Here plotted by Ken Monks
answered Feb 9 '15 at 21:11
GEdgarGEdgar
63.7k269176
$endgroup$
add a comment |
$begingroup$
Maybe the "Pharaoh's Breastplate" described by Mandelbrot.
Here plotted by Ken Monks
answered Feb 9 '15 at 21:11
GEdgarGEdgar
63.7k269176
$endgroup$
Maybe the "Pharaoh's Breastplate" described by Mandelbrot.
Here plotted by Ken Monks
answered Feb 9 '15 at 21:11
GEdgarGEdgar
63.7k269176
answered Feb 9 '15 at 21:11
GEdgarGEdgar
63.7k269176
answered Feb 9 '15 at 21:11
GEdgarGEdgar
63.7k269176
answered Feb 9 '15 at 21:11
GEdgarGEdgar
63.7k269176
63.7k269176
add a comment |
add a comment |
$begingroup$
If you draw 6 smaller circles inside each circle you draw... you end up with something like a
My rendering only draws 6 iterations deep - but you could theoretically go forever.
edited Jan 14 at 22:02
Xander Henderson
15.2k103556
answered Jan 14 at 21:31
Tom HTom H
111
$endgroup$
1
$begingroup$
That construction is usually called the "hexagasket". It is a specific example of a general construction called an "$n$-gasket" (in case you are looking for things to Google).
$endgroup$
– Xander Henderson
Jan 14 at 22:01
add a comment |
$begingroup$
If you draw 6 smaller circles inside each circle you draw... you end up with something like a
My rendering only draws 6 iterations deep - but you could theoretically go forever.
edited Jan 14 at 22:02
Xander Henderson
15.2k103556
answered Jan 14 at 21:31
Tom HTom H
111
$endgroup$
1
$begingroup$
That construction is usually called the "hexagasket". It is a specific example of a general construction called an "$n$-gasket" (in case you are looking for things to Google).
$endgroup$
– Xander Henderson
Jan 14 at 22:01
add a comment |
$begingroup$
If you draw 6 smaller circles inside each circle you draw... you end up with something like a
My rendering only draws 6 iterations deep - but you could theoretically go forever.
edited Jan 14 at 22:02
Xander Henderson
15.2k103556
answered Jan 14 at 21:31
Tom HTom H
111
$endgroup$
If you draw 6 smaller circles inside each circle you draw... you end up with something like a
My rendering only draws 6 iterations deep - but you could theoretically go forever.
edited Jan 14 at 22:02
Xander Henderson
15.2k103556
answered Jan 14 at 21:31
Tom HTom H
111
edited Jan 14 at 22:02
Xander Henderson
15.2k103556
edited Jan 14 at 22:02
Xander Henderson
15.2k103556
edited Jan 14 at 22:02
Xander Henderson
15.2k103556
15.2k103556
answered Jan 14 at 21:31
Tom HTom H
111
answered Jan 14 at 21:31
Tom HTom H
111
answered Jan 14 at 21:31
Tom HTom H
111
111
1
$begingroup$
That construction is usually called the "hexagasket". It is a specific example of a general construction called an "$n$-gasket" (in case you are looking for things to Google).
$endgroup$
– Xander Henderson
Jan 14 at 22:01
add a comment |
1
$begingroup$
That construction is usually called the "hexagasket". It is a specific example of a general construction called an "$n$-gasket" (in case you are looking for things to Google).
$endgroup$
– Xander Henderson
Jan 14 at 22:01
1
1
$begingroup$
That construction is usually called the "hexagasket". It is a specific example of a general construction called an "$n$-gasket" (in case you are looking for things to Google).
$endgroup$
– Xander Henderson
Jan 14 at 22:01
$begingroup$
That construction is usually called the "hexagasket". It is a specific example of a general construction called an "$n$-gasket" (in case you are looking for things to Google).
$endgroup$
– Xander Henderson
Jan 14 at 22:01
add a comment |
Thanks for contributing an answer to Mathematics Stack Exchange!
- Please be sure to answer the question. Provide details and share your research!
But avoid …
- Asking for help, clarification, or responding to other answers.
- Making statements based on opinion; back them up with references or personal experience.
Use MathJax to format equations. MathJax reference.
To learn more, see our tips on writing great answers.
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function () {
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmath.stackexchange.com%2fquestions%2f1140989%2fis-there-a-koch-circle%23new-answer', 'question_page');
}
);
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
4
$begingroup$
I'm not sure of all the details you want, but anything you can imagine or roughly draw could certainly be "fractalized", but there remains the question of why someone would want to study it. Possible close to what you want might be Apollonian Gasket, however.
$endgroup$
– Dave L. Renfro
Feb 9 '15 at 19:35
1
$begingroup$
An apollonian gasket comes close to what I imagine, yes! I honestly don't know a reason to study it, aside that it maybe beautiful(probably not as beautiful as the gasket).
$endgroup$
– user2103480
Feb 9 '15 at 20:27
$begingroup$
Apollonian Gasket seems like the best answer so far.
$endgroup$
– alan2here
May 21 '17 at 17:42